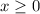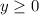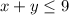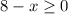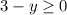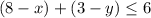Answer:
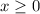
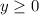
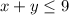
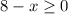
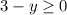
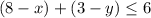
Explanation:
Given
x = Cars from Baltimore to Trenton
y = Cars from Baltimore to Philadelphia
Required
Write out 6 inequalities
First, 0 or more cars must be shipped to both locations
So:
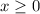
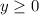
Considering the warehouse in Baltimore.
(1) The warehouse can not ship more than the number of car it has (9).
So:
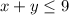
Considering the warehouse in New York.
(1) After shipping cars to Trenton and Philadelphia, the warehouse will have 0 or more cars.
So:
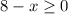 --- To Trenton
--- To Trenton
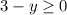 --- To Philadelphia
--- To Philadelphia
(2) The warehouse cannot send out more than 6.
So:
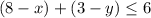
So, the inequalities are: