Answer:
A. 0.2734 = 27.34% probability that there are an equal number of boys and girls
B. 0.2753 = 27.53% probability that she’ll answer exactly 5 questions correctly
Explanation:
In each of these questions, the binomial probability distribution is used.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

In which
 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.

And p is the probability of X happening.
A.The Murray family has produced 8 children.
What is the probability that there are an equal number of boys and girls?
8 children means that

Each children is equally as likely to be a boy or a girl, which means that
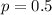
This probability is P(X = 4). So

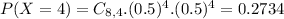
0.2734 = 27.34% probability that there are an equal number of boys and girls
B.Margie has the uncanny ability of being able to guess the correct answer to TRUE/FALSE questions with an 80% accuracy rate. Tomorrow’s test has 7 questions on it and she needs to answer 5 questions correctly in order to make the Honor Roll. If she guesses on every question, what is the probability that she’ll answer exactly 5 questions correctly?
80% accurracy rate means that
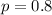
7 questions means that
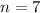
The probability is P(X = 5). So

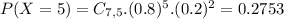
0.2753 = 27.53% probability that she’ll answer exactly 5 questions correctly