Question

The mean heigh of American Males is 69.5 inches. The height of the 43 male presidents have a mean 70.78 inches and a standard deviation of 2.77 inches. Treating the 43 presidents as a simple random sample, determine if there is evidence to suggest that the US presidents are taller than the average American male. Use the a= 0.05 level of significance.

Answer 1

To determine if the US presidents are taller than the average American male, a one-sample t-test is conducted. The null hypothesis is that the mean height of the presidents is equal to the mean height of American males, while the alternative hypothesis is that the mean height of the presidents is greater. Using a significance level of 0.05, the test statistic is compared to the critical value to make a conclusion.

Step-by-step explanation:

To determine if there is evidence to suggest that the US presidents are taller than the average American male, we can conduct a hypothesis test. The null hypothesis is that the mean height of the presidents is equal to the mean height of American males (69.5 inches), and the alternative hypothesis is that the mean height of the presidents is greater than the mean height of American males.

We can use a one-sample t-test to compare the sample mean height of the presidents (70.78 inches) to the population mean height of American males (69.5 inches). With a sample size of 43, the degrees of freedom are 42.

Using a significance level of 0.05, we can compare the test statistic (t) to the critical value from the t-distribution with 42 degrees of freedom. If the t-value is greater than the critical value, we reject the null hypothesis and conclude that there is evidence to suggest that the US presidents are taller than the average American male.

Answer 2

There is sufficient statistical evidence to suggest that the US presidents are taller than the average American male

Step-by-step explanation:

The given parameters are;

The mean height of American Males, μ = 69.5 inches

The mean height of 43 male presidents,
`\overline x` = 70.78

The standard deviation, s = 2.77 inches

The number of male presidents = 43

The null hypothesis; H₀ μ =
`\overline x`

The alternative hypothesis; Hₐ μ ≠
`\overline x`

The significance level, α = 0.05

The t test for the sample with unknown population standard deviation is given as follows;

`t=\frac{\bar{x}-\mu }{(s )/(√(n))}`

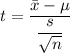
Therefore, we have;

`t=(70.78-69.5 )/((2.77 )/(√(43))) \approx 3.0302`

The degrees of freedom, df = n - 1 = 43 - 1 = 42

The critical 't' value = 2.0181

Therefore, given that the t test value is larger than the critical-t, we reject the null hypothesis, therefore, there is sufficient statistical evidence to suggest that the US presidents are taller than the average American male