Question

The following information was obtained from independent random samples taken of two populations. Assume normally distributed populations with equal variances. Sample 1 Sample 2 Sample Mean 45 42 Sample Variance 85 90 Sample Size 10 12 The 95% confidence interval for the difference between the two population means is (use rounded standard error) a. -2.65 to 8.65. b. -5.344 to 11.344. c. -5 to 3. d. -4.86 to 10.86.

Answer 1

95% Confidence Interval is; ( -5.344 to 11.344 )

Option b) -5.344 to 11.344 is the correct answer

Explanation:

Given the data in the question;

Sample 1 Sample 2

x"₁ = 45 x"₂ = 42

S₁² = 85 S₂² = 90

n₁ = 10 n₂ = 12

df = [ S₁²/n₁ + S₂²/n₂ ]² / [ ((S₁²/n₁)²/n₁-1) + ((S₂²/n₂)²/n₂-1)) ]

we substitute

df = [ 10/10 + 90/12 ]² / [ ((85/10)²/10-1) + ((90/12)²/12-1)) ] = 19.64 ≈ 20

df = 20

with 95% confidence interval

∝ = 1 - 0.95 = 0.05

∝/2 = 0.05/2 = 0.025

now,
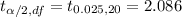`t_(\alpha /2,df) = t_(0.025, 20) = 2.086` { from table }

95% confidence interval for N1 - N2

⇒ (x"₁ - x"₂) ±
`t_(\alpha /2,df)` × √( S₁²/n₁ + S₂²/n₂ )

⇒ (45 - 42) ± 2.086 × √( 85/10 + 90/12 )

⇒ 3 ± 2.086 × 4

⇒ 3 ± 8.344

so;

Lower Limit = 3 - 8.344 = -5.344

Upper Limit = 3 + 8.344 = 11.344

Therefore, 95% Confidence Interval is; ( -5.344 to 11.344 )

Option b) -5.344 to 11.344 is the correct answer