Question

An engineer is going to redesign an ejection seat for an airplane. The seat was designed for pilots weighing between 140 lb and 191 lb. The new population of pilots has normally distributed weights with a mean of 148 lb and a standard deviation of 30.3 lb.

a. If a pilot is randomly​ selected, find the probability that his weight is between 140 lb and 191 lb.

The probability is approximately _____. ​(Round to four decimal places as​ needed.)

Answer 1

The probability is approximately 0.3193

Explanation:

The question parameters;

The mass between of the pilot for which the seat was designed,
`\overline x` = 140 lb and 191 lb

The mean weight of the new pilots, μ = 148 lb

The standard deviation of the weights new pilots, s = 30.3 lb

a. The z-score is given as follows;

`z=\frac{\bar{x}-\mu }{{\sigma }}`

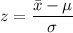
Therefore, we have;

`z_(140)=\frac{140-148 }{{30.3 }} \approx 0.264\overline {0264}`

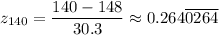
The p-value = 0.60257

`z_(191)=\frac{191-148 }{{30.3 }} \approx 1.419\overline {1419}`

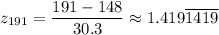
The p-value = 0.9222

The probability that the mean lie between the two values = 0.9222 - 0.60257 = 0.31963

Therefore, the probability that the weight is between the 140 lb and 191 lb ≈ 0.3196