Question

The function that passes through the points (24, 28) and (8,8)​

Answer 1

The student is looking for the equation of a linear function that passes through the points (24, 28) and (8, 8). The equation is discovered by first determining the slope using the given points, then employing the point-slope form, and finally converting it to slope-intercept form.

Step-by-step explanation:

The student is asking for the equation of the linear function that passes through the given points (24, 28) and (8, 8). To determine the equation of a line, we need to calculate the slope (m) and use one of the points for the y-intercept (b) if necessary.

Step 1: Calculate the slope (m) using the formula: m = (y2 - y1) / (x2 - x1).

Step 2: Use the slope and one of the points in the point-slope form of the equation of a line, which is y - y1 = m(x - x1), to find the equation in slope-intercept form (y = mx + b).

Step 3: Calculate the y-intercept (b) if required and write the final equation of the line.

Answer 2

`y=1.25x-2`

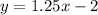
Step-by-step explanation:

The function I used was a linear function (
`y=mx+b`). I found the slope and y-intercept by going to my calculator and doing these steps:

1. Turn on the calculator

2. Press the STAT button

3. Select Edit . . .

And the calculator will show an empty data table. If there are already numbers in the data table:

1. Click STAT again

2. Select ClrList

3. Press 2nd and number 1

4. Select the comma, it's above 7

5. Press 2nd and number 2

6. Hit enter

Finally, after entering the numbers into the data table in their according spots, you then:

1. Press STAT

2. Go to CALC and Select LinReg (ax+b)

3. And hit enter 5 times, and you'll get your answer

y = -2

m = 1.25