Answer:
The length of the third piece of the ramp is;
D. 9.24 feet
Explanation:
The given parameters are;
The height of the ramp = 8 feet
The angle between the piece that forms height and the base = 90°
The angle formed by the third piece connecting the height of the ramp to the furthest point and the 8 foot piece = 30°
Let 'y' represent the 8-foot piece forming the height, and let 'r' represent the third piece, by trigonometric ratio, we have;
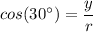
Therefore, we get;
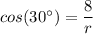
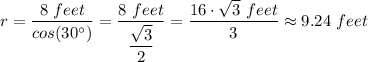
The length of the third piece, r ≈ 9.24 feet