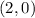Three vertices of parallelogram DEFG are D(-4,-2), E(-3,1) and F(3, 3). Find the coordinates of G. The coordinates of G are

Question

asked Nov 2, 2022 35.8k views

1 Answer

Davir · Answer 1 · 2022-11-09T15:48:25+0000

Answer:

Coordinates of G =
(2,0)

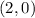
Explanation:

Given: Three vertices of parallelogram DEFG are D(-4,-2), E(-3,1) and F(3, 3).

To find: coordinates of G

Solution:

Midpoints of a side joining points
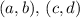$(a,b),\,(c,d)$ are given by
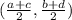
((a+c)/(2),(b+d)/(2))

Diagonals of a parallelogram bisect each other.

So,

Midpoint of DF = Midpoint of EG

Midpoint of DF =
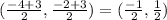
((-4+3)/(2),(-2+3)/(2))=((-1)/(2),(1)/(2))

Midpoint of EG =
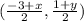
((-3+x)/(2),(1+y)/(2))

Let coordinates of G be
(x,y)

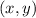
Therefore,

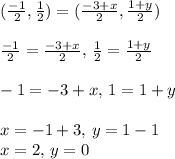
$((-1)/(2),(1)/(2)) =((-3+x)/(2),(1+y)/(2))\\\\(-1)/(2)=(-3+x)/(2),\,(1)/(2)=(1+y)/(2)\\\\-1=-3+x,\,1=1+y\\\\x=-1+3,\,y=1-1\\x=2,\,y=0$

So,

Coordinates of G =
(2,0)