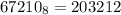Question

Note: You can use a word document to write your answers and copy-paste your answer to the area specified. a. (5 points) Convert the following base 16 numbers to base 10. Show your calculation steps. EA916 CB216 b. (5 points) Convert the following binary numbers to base 10. Show your calculation steps. (The space between numbers is left to make the reading easy.) (1011 1110 1101 1011 1010)2 (1010 1000 1011 1000 1110 1101)2 c. (5 points) Convert the following binary numbers to base 16. Show your calculation steps. i. (1011 1110 1101 1011 1010)2 ii. (1010 1000 1011 1000 1110 1101)2 d. (5 points) Convert the following decimal number to octal. i. 74510 ii. 67210

Answer 1

`EA9_(16) = 3753`

`CB2_(16) = 3250`

`(1011 1110 1101 1011 1010)_2 = 781754`

`(1010 1000 1011 1000 1110 1101)_2 = 11057389`

`(1011 1110 1101 1011 1010)_2 = BEDBA`

`(1010 1000 1011 1000 1110 1101)_2 = A8B8ED`

`74510_8= 221416`

`67210_8 = 203212`

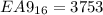
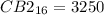
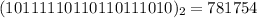
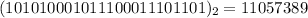
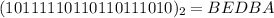
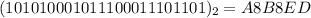
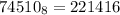
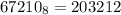
Step-by-step explanation:

Solving (a): To base 10

`(i)\ EA9_{16`

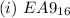
We simply multiply each digit by a base of 16 to the power of their position.

i.e.

`EA9_(16) = E * 16^2 + A * 16^1 + 9 * 16^0`

`EA9_(16) = E * 256 + A * 16 + 9 * 1`

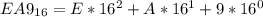
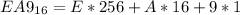
In hexadecimal

`A = 10; E = 14`

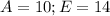
So:

`EA9_(16) = 14 * 256 + 10 * 16 + 9 * 1`

`EA9_(16) = 3753`

`(ii)\ CB2_(16)`

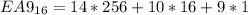
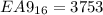
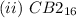
This gives:

`CB2_(16) = C * 16^2 + B * 16^1 + 2 * 16^0`

`CB2_(16) = C * 256 + B * 16 + 2 * 1`

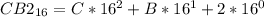
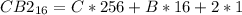
In hexadecimal

`C = 12; B =11`

So:

`CB2_(16) = 12 * 256 + 11 * 16 + 2 * 1`

`CB2_(16) = 3250`

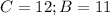
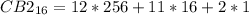
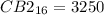
Solving (b): To base 10

`(i)\ (1011 1110 1101 1011 1010)_2`

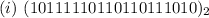
We simply multiply each digit by a base of 2 to the power of their position.

i.e.

`(1011 1110 1101 1011 1010)_2 = 1 * 2^(19) + 0 * 2^(18) + 1 * 2^(17) + 1 * 2^(16) +1 * 2^(15) + 1 * 2^(14) + 1 * 2^(13) + 0 * 2^(12) + 1 * 2^(11) + 1 * 2^(10) + 0 * 2^9 + 1 * 2^8 +1 * 2^7 + 0 * 2^6 + 1 * 2^5 + 1 * 2^4 + 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 0 * 2^0`

`(1011 1110 1101 1011 1010)_2 = 781754`

`(ii)\ (1010 1000 1011 1000 1110 1101)_2`

`(1010 1000 1011 1000 1110 1101)_2 = 1 * 2^(23) + 0 * 2^(22) + 1 * 2^(21) + 0 * 2^(20) +1 * 2^(19) + 0 * 2^(18) + 0 * 2^(17) + 0 * 2^(16) + 1 * 2^(15) + 0 * 2^(14) + 1 * 2^(13) + 1 * 2^(12) +1 * 2^(11) + 0 * 2^(10) + 0 * 2^9 + 0 * 2^8 + 1 * 2^7 + 1 * 2^6 + 1 * 2^5 + 0 * 2^4 + 1*2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0`

`(1010 1000 1011 1000 1110 1101)_2 = 11057389`

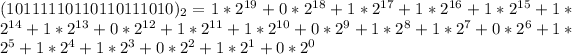
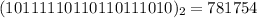
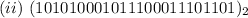
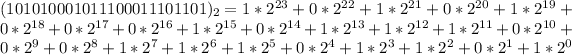
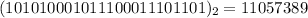
Solving (c): To base 16

`i.\ (1011 1110 1101 1011 1010)_2`

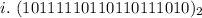
First, convert to base 10

In (b)

`(1011 1110 1101 1011 1010)_2 = 781754`

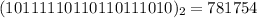
Next, is to divide 781754 by 16 and keep track of the remainder

`781754/16\ |\ 48859\ R\ 10`

`48859/16\ |\ 3053\ R\ 11`

`3053/16\ |\ 190\ R\ 13`

`190/16\ |\ 11\ R\ 14`

`11/16\ |\ 0\ R\ 11`

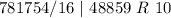
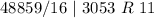
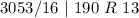
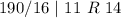
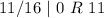
Write out the remainder from bottom to top

`(11)(14)(13)(11)(10)`

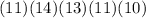
In hexadecimal

`A = 10; B = 11; C = 12; D = 13; E = 14; F = 15.`

`(11)(14)(13)(11)(10)=BEDBA`

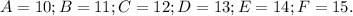
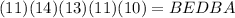
So:

`(1011 1110 1101 1011 1010)_2 = BEDBA`

`ii.\ (1010 1000 1011 1000 1110 1101)_2`

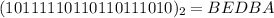
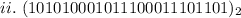
In b

`(1010 1000 1011 1000 1110 1101)_2 = 11057389`

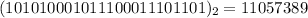
Next, is to divide 11057389 by 16 and keep track of the remainder

`11057389/16\ |\ 691086\ R\ 13`

`691086/16\ |\ 43192\ R\ 14`

`43192/16\ |\ 2699\ R\ 8`

`2699/16\ |\ 168\ R\ 11`

`168/16\ |\ 10\ R\ 8`

`10/16\ |\ 0\ R\ 10`

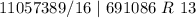
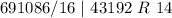
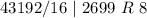
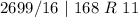
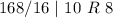
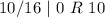
Write out the remainder from bottom to top

`(10)8(11)8(14)(13)`

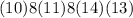
In hexadecimal

`A = 10; B = 11; C = 12; D = 13; E = 14; F = 15.`

`(10)8(11)8(14)(13) = A8B8ED`

So:

`(1010 1000 1011 1000 1110 1101)_2 = A8B8ED`

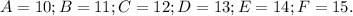
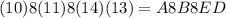
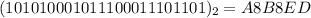
Solving (d): To octal

`(i.)\ 74510`

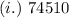
Divide 74510 by 8 and keep track of the remainder

`74510/8\ |\ 9313\ R\ 6`

`9313/8\ |\ 1164\ R\ 1`

`1164/8\ |\ 145\ R\ 4`

`145/8\ |\ 18\ R\ 1`

`18/8\ |\ 2\ R\ 2`

`2/8\ |\ 0\ R\ 2`

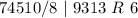
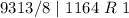
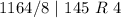
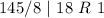
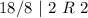
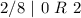
Write out the remainder from bottom to top

`74510_8= 221416`

`(ii.)\ 67210`

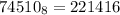
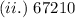
Divide 67210 by 8 and keep track of the remainder

`67210/8\ |\ 8401\ R\ 2`

`8401/8\ |\ 1050\ R\ 1`

`1050/8\ |\ 131\ R\ 2`

`131/8\ |\ 16\ R\ 3`

`16/8\ |\ 2\ R\ 0`

`2/8\ |\ 0\ R\ 2`

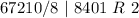
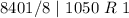
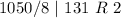
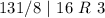
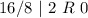
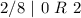
Write out the remainder from bottom to top

`67210_8 = 203212`