Question

Compute f’(x) if f(x)= x^cosx

Answer 1

We are given with a function and have to find it's Derivative , So let's start !!

`{:\implies \quad \sf f(x)=x^(\cos (x))}`

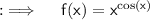
Take Natural log on both sides ;

`{:\implies \quad \sf ln\{f(x)\}=ln\{x^(\cos (x))\}}`

`{:\implies \quad \sf ln\{f(x)\}=\cos (x)ln(x)\quad \qquad \{\because ln(a^(b))=b\: ln(a)\}}`

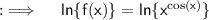
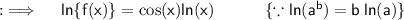
Differentiating both sides w.r.t.x ;

`{:\implies \quad \sf (1)/(f(x))\cdot f^(\prime)(x)=(d)/(dx)\bigg\{\cos (x)\cdot ln(x)\bigg\}}`

Using Leibnitz's Product rule ;

`{:\implies \quad \sf f^(\prime)(x)=f(x)\left[(d)/(dx)\{\cos (x)\}\cdot ln(x)+(d)/(dx)\{ln(x)\}\cdot \cos (x)\right]}`

`{:\implies \quad \sf f^(\prime)(x)=x^(\cos (x))\bigg\{- \sin (x)ln(x)+(\cos (x))/(x)\bigg\}}`

`{:\implies \quad \bf \therefore \quad \underline{\underline{f^(\prime)(x)=x^(\cos (x))\bigg\{(\cos (x))/(x)- \sin (x)ln(x)\bigg\}}}}`

Used Concepts :-

• 
  `{\bf (d)/(dx)\{ln(x)\}=\frac1x}`

• 
  `{\bf (d)/(dx)\{\cos (x)\}=- \sin (x)}`

Leibnitz's Product Rule of differentiation :-

• 
  `{\quad \boxed{\bf{(d)/(dx)(uv)=v(du)/(dx)+u(dv)/(dx)}}}`

Where , u & v both are functions of x .

Answer 2

Hi there!

`f(x) = x^(cosx)`

We can rewrite as:

`y = x^(cosx)`

Take the natural log of both sides.

`lny = cos(x)ln(x)`

Now, differentiate both sides. Recall the product rule:

`(d)/(dx)f(x) * g(x) = f'(x)g(x) + g'(x)f(x)`

`f(x) = cos(x)\\\\g(x) = ln(x)`

And the natural log rule:

`(dy)/(dx) (lnx) = (1)/(x)`

Using these rules:

`(1)/(y)(dy)/(dx) = cos(x)((1)/(x)) -sin(x)ln(x)`

Multiply both sides by y.

`(dy)/(dx) = y(cos(x)((1)/(x)) -sin(x)ln(x))`

Since we cannot have a 'y' in the equation, we can substitute in the original expression above:

`y = x^(cosx)\\\\`

Thus:

`(dy)/(dx) = x^(cosx)(cos(x)((1)/(x)) -sin(x)ln(x))`

`\boxed{(dy)/(dx) = x^(cosx)((cos(x))/(x) -sin(x)ln(x))}`