Answer:
The angular speed is 23.24 rad/s.
Step-by-step explanation:
Given;
mass of the disk, m = 7 kg
radius of the disk, r = 0.2 m
applied force, F = 42 N
distance moved by disk, d = 0.9 m
The torque experienced by the disk is calculated as follows;
τ = F x d = I x α
where;
I is the moment of inertia of the disk = ¹/₂mr²
α is the angular acceleration
F x r = ¹/₂mr² x α
The angular acceleration is calculated as;
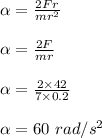
The angular speed is determined by applying the following kinematic equation;
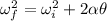
initial angular speed, ωi = 0
angular distance, θ = d/r = 0.9/0.2 = 4.5 rad
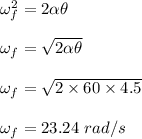
Therefore, the angular speed is 23.24 rad/s.