Question

All the fourth-graders in a certain elementary school took a standardized test. A total of 82% of the students were found to be proficient in reading, 74% were found to be proficient in mathematics, and 65% were found to be proficient in both reading and mathematics.A student is chosen at random. What is the probability that the student is proficient in neither reading nor mathematics

Answer 1

0.09 = 9% probability that the student is proficient in neither reading nor mathematics

Explanation:

We solve this question treating the events as Venn probabilities.

I am going to say that:

Event A: A student is proficient in reading.

Event B: A student is proficient in mathematics.

A total of 82% of the students were found to be proficient in reading

This means that
`P(A) = 0.82`

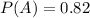
74% were found to be proficient in mathematics

This means that
`P(B) = 0.74`

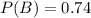
65% were found to be proficient in both reading and mathematics.

This means that
`P(A \cap B) = 0.65`

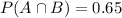
What is the probability that the student is proficient in neither reading nor mathematics?

This is:

`P = 1 - P(A \cup B)`

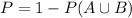
In which

`P(A \cup B) = P(A) + P(B) - P(A \cap B)`

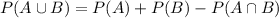
With the values that we have:

`P(A \cup B) = 0.82 + 0.74 - 0.65 = 0.91`

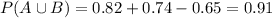
Then

`P = 1 - P(A \cup B) = 1 - 0.91 = 0.09`

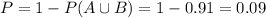
0.09 = 9% probability that the student is proficient in neither reading nor mathematics