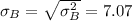Answer:
The answer is "
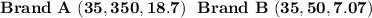 "
"
Step-by-step explanation:
Calculating the mean for brand A:
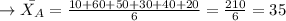
Calculating the Variance for brand A:
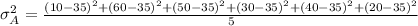
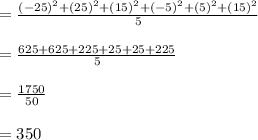
Calculating the Standard deviation:
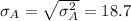
Calculating the Mean for brand B:
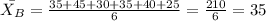
Calculating the Variance for brand B:
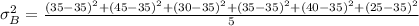

Calculating the Standard deviation: