Question

Whoops i forgot to read the lesson :P 30 points

Answer 1

Explanation:

I'll do 2.

Alright,Alex let say we have factored a quadratic into two binomial, for example

`(5x + 3)(6x - 4)`

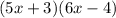
If we set both of those equal to zero

`(5x + 3)(6x + 4) = 0`

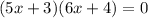
We can used the zero product property in this case to find the roots of the quadratic equation.

This means that

`if \: ab = 0 \: then \: a = 0 \: and \: b = 0`

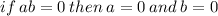
This means we set each binomal equal to zero to find it root.

`5x + 3 = 0`

`5x = - 3`

`x = - (3)/(5)`

`6x + 4 = 0`

`6x = - 4`

`x = - (2)/(3)`

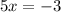
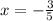
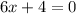
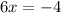
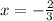
So our roots are negative 3/5 and negative 2/3 using zero product property