Question

Find the area of the region enclosed by the graphs of the functions

f(x)=x^2, g(x)=x^6
by partitioning the x- axis.
(Use symbolic notation and fractions where needed.)

Answer 1

`\displaystyle A = (8)/(21)`

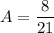
General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Equality Properties

• Multiplication Property of Equality
• Division Property of Equality
• Addition Property of Equality
• Subtraction Property of Equality

Algebra I

• Terms/Coefficients
• Functions
• Function Notation
• Graphing
• Solving systems of equations

Calculus

Area - Integrals

Integration Rule [Reverse Power Rule]:
`\displaystyle \int {x^n} \, dx = (x^(n + 1))/(n + 1) + C`

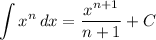
Integration Rule [Fundamental Theorem of Calculus 1]:
`\displaystyle \int\limits^b_a {f(x)} \, dx = F(b) - F(a)`

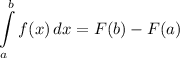
Integration Property [Addition/Subtraction]:
`\displaystyle \int {[f(x) \pm g(x)]} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx`

Area of a Region Formula:
`\displaystyle A = \int\limits^b_a {[f(x) - g(x)]} \, dx`

Explanation:

*Note:

Remember that for the Area of a Region, it is top function minus bottom function.

Step 1: Define

f(x) = x²

g(x) = x⁶

Bounded (Partitioned) by x-axis

Step 2: Identify Bounds of Integration

Find where the functions intersect (x-values) to determine the bounds of integration.

Simply graph the functions to see where the functions intersect (See Graph Attachment).

Interval: [-1, 1]

Lower bound: -1

Upper Bound: 1

Step 3: Find Area of Region

Integration

1. Substitute in variables [Area of a Region Formula]:
   `\displaystyle A = \int\limits^1_(-1) {[x^2 - x^6]} \, dx`
2. [Area] Rewrite [Integration Property - Subtraction]:
   `\displaystyle A = \int\limits^1_(-1) {x^2} \, dx - \int\limits^1_(-1) {x^6} \, dx`
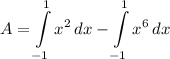
3. [Area] Integrate [Integration Rule - Reverse Power Rule]:
   `\displaystyle A = (x^3)/(3) \bigg| \limit^1_(-1) - (x^7)/(7) \bigg| \limit^1_(-1)`
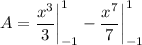
4. [Area] Evaluate [Integration Rule - FTC 1]:
   `\displaystyle A = (2)/(3) - (2)/(7)`
5. [Area] Subtract:
   `\displaystyle A = (8)/(21)`

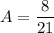
Topic: AP Calculus AB/BC (Calculus I/II)

Unit: Area Under the Curve - Area of a Region (Integration)

Book: College Calculus 10e