Question

Find the area of the region enclosed by the graphs of these equations. (CALCULUS HELP)

Answer 1

The area of the region enclosed by the graphs can be found by calculating the integral of the function describing the boundary, or using geometric formulas if shapes are simple like triangles or rectangles.

Step-by-step explanation:

The area of the region enclosed by the graphs of given equations can be found using calculus principles, specifically through integration. Depending on the shape of the region, different geometric formulae, such as the area of a triangle or a rectangle, may apply. However, if the boundary of the region is a curve described by a function, the area can be calculated as the integral of the function over the interval enclosed by the curve.

For example, if you have a velocity-time graph, and you wish to find the displacement over a certain time interval, you would calculate the area under the curve during that interval. If the graph is a straight line (which signifies constant acceleration), the shape formed is a right triangle, and its area can be found using the formula for the area of a right triangle (½ * base * height).

Answer 2

`\displaystyle A = (20√(15))/(3)`

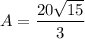
General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Equality Properties

1. Multiplication Property of Equality
2. Division Property of Equality
3. Addition Property of Equality
4. Subtraction Property of Equality

Algebra I

• Terms/Coefficients
• Graphing
• Exponential Rule [Root Rewrite]:
  `\displaystyle \sqrt[n]{x} = x^{(1)/(n)}`

Calculus

Derivatives

Derivative Notation

Derivative of a constant is 0

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Area - Integrals

U-Substitution

Integration Rule [Reverse Power Rule]:
`\displaystyle \int {x^n} \, dx = (x^(n + 1))/(n + 1) + C`

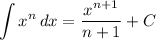
Integration Property [Multiplied Constant]:
`\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx`

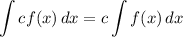
Integration Property [Addition/Subtraction]:
`\displaystyle \int {[f(x) \pm g(x)]} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx`

Integration Rule [Fundamental Theorem of Calculus 1]:
`\displaystyle \int\limits^b_a {f(x)} \, dx = F(b) - F(a)`

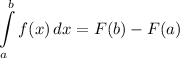
Area of a Region Formula:
`\displaystyle A = \int\limits^b_a {[f(x) - g(x)]} \, dx`

Step-by-step explanation:

Step 1: Define

F: y = √(15 - x)

G: y = √(15 - 3x)

H: y = 0

Step 2: Find Bounds of Integration

Solve each equation for the x-value for our bounds of integration.

F

1. Set y = 0: 0 = √(15 - x)
2. [Equality Property] Square both sides: 0 = 15 - x
3. [Subtraction Property of Equality] Isolate x term: -x = -15
4. [Division Property of Equality] Isolate x: x = 15

G

1. Set y = 0: 0 = √(15 - 3x)
2. [Equality Property] Square both sides: 0 = 15 - 3x
3. [Subtraction Property of Equality] Isolate x term: -3x = -15
4. [Division Property of Equality] Isolate x: x = 5

This tells us that our bounds of integration for function F is from 0 to 15 and our bounds of integration for function G is 0 to 5.

We see that we need to subtract function G from function F to get our area of the region (See attachment graph for visual).

Step 3: Find Area of Region

Integration Part 1

1. Rewrite Area of Region Formula [Integration Property - Subtraction]:
   `\displaystyle A = \int\limits^b_a {f(x)} \, dx - \int\limits^d_c {g(x)} \, dx`
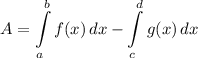
2. [Integral] Substitute in variables and limits [Area of Region Formula]:
   `\displaystyle A = \int\limits^(15)_0 {√(15 - x)} \, dx - \int\limits^5_0 {√(15 - 3x)} \, dx`
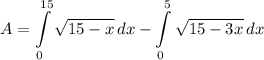
3. [Area] [Integral] Rewrite [Exponential Rule - Root Rewrite]:
   `\displaystyle A = \int\limits^(15)_0 {(15 - x)^{(1)/(2)}} \, dx - \int\limits^5_0 {(15 - 3x)^{(1)/(2)}} \, dx`

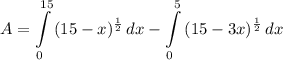
Step 4: Identify Variables

Set variables for u-substitution for both integrals.

Integral 1:

u = 15 - x

du = -dx

Integral 2:

z = 15 - 3x

dz = -3dx

Step 5: Find Area of Region

Integration Part 2

1. [Area] Rewrite [Integration Property - Multiplied Constant]:
   `\displaystyle A = -\int\limits^(15)_0 {-(15 - x)^{(1)/(2)}} \, dx + (1)/(3)\int\limits^5_0 {-3(15 - 3x)^{(1)/(2)}} \, dx`
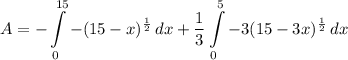
2. [Area] U-Substitution:
   `\displaystyle A = -\int\limits^0_(15) {u^{(1)/(2)}} \, du + (1)/(3)\int\limits^0_(15) {z^{(1)/(2)}} \, dz`
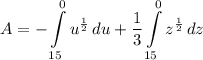
3. [Area] Reverse Power Rule:
   `\displaystyle A = -(\frac{2u^{(3)/(2)}}{3}) \bigg|\limit^0_(15) + (1)/(3)(\frac{2z^{(3)/(2)}}{3}) \bigg|\limit^0_(15)`
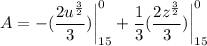
4. [Area] Evaluate [Integration Rule - FTC 1]:
   `\displaystyle A = -(-10√(15)) + (1)/(3)(-10√(15))`
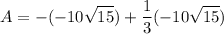
5. [Area] Multiply:
   `\displaystyle A = 10√(15) + (-10√(15))/(3)`
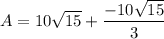
6. [Area] Add:
   `\displaystyle A = (20√(15))/(3)`

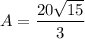
Topic: AP Calculus AB/BC (Calculus I/II)

Unit: Area Under the Curve - Area of a Region (Integration)

Book: College Calculus 10e