Question

Please help!

(Vieta's Formulas) Let
`r`,
`s`, and
`t` be solutions to the equation
`$2x^3 - 3x^2 + 4x - 1 = 0$`. Find
`$r^2+s^2+t^2$`.


Please include an explanation as well :)

Answer 1

We are given the polynomial:

2x³ - 3x² + 4x - 1 = 0

We need to find the value of r² + s² + t² where r,s,t are the solutions.

Simplifying r² + s² + t²:

r² + s² + t² = (r + s + t)² - 2(rs + st + rt)

[since a²+b²+c² = (a+b+c)² - 2(ab + bc + ca)]

Using the Vieta's formulae:

Above, we can see that in order to find the value of r² + s² + t², we need to find the value of the sum of solutions and sum of solutions taken 2 at a time.

Sum of roots:

We know that the Vieta's formula to find the sum of roots is:

Sum of roots =
`-(b)/(a)`

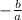
Where b and a are the coefficients from the general form: ax³ + bx² + cx - d

We notice that for the given equation, b = -3 ; a = 2

Sum of roots =
`-((-3)/(2))`

Sum of roots =
`(3)/(2)`

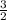
Hence, the sum of roots (r + s + t) = 3/2

Sum of roots taken two at a time:

We know that the Vieta's formula to find the sum of roots taken 2 at a time is: Sum of roots taken 2 at a time =
`(c)/(a)`

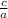
Where c and a are the coefficients from the general form: ax³ + bx² + cx - d

for the given equation, c = 4 ; a = 2

Sum of roots taken 2 at a time =
`(4)/(2)`

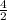
Sum of roots taken 2 at a time = 2

Hence, the sum of roots taken 2 at a time (rs + st + rt) = 2

Finding the value of r² + s² + t²:

We proved before that:

r² + s² + t² = (r + s + t)² - 2(rs + st + rt)

now that we know the values of (r + s + t) and (rs + st + rt), we can plug those values to get our answer

r² + s² + t² = (
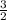`(3)/(2)`)² - 2(2)

r² + s² + t² = (
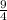`(9)/(4\\)`) - 4

r² + s² + t² =
`(9 - 16)/(4\\)`

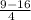
r² + s² + t² =
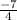`(-7)/(4)` = -1.75

Hence, the value of r² + s² + t² is -1.75