Question

Two cards are drawn without replacement from a standard deck of 5252 playing cards. What is the probability of choosing a heart and then, without replacement, a spade? Express your answer as a fraction or a decimal number rounded to four decimal places

Answer 1

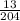`(13)/(204)` ≈ 0.0637

Explanation:

Given: Two cards are drawn without replacement from a standard deck of 52 playing cards.

To find: probability of choosing a heart and then, without replacement, a spade

Solution:

Probability refers to chance of occurrence of any event.

Probability = Number of favorable outcomes ÷ Total number of outcomes

Total number of cards = 52

Number of hearts = 13

So,

probability of choosing a heart =
`(13)/(52)=(1)/(4)`

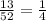
Number of remaining cards =
`52-1=51`

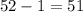
Number of spades = 13

Probability of choosing a spade =
`(13)/(51)`

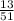
Events consisting of choosing a heart and spade are independent.

So,

Probability of choosing a heart and then, without replacement, a spade =

Probability of choosing a heart × Probability of choosing a spade

=
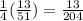`(1)/(4)((13)/(51))=(13)/(204)` ≈ 0.0637