Answer:
θ =
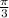 (60° )
(60° )
Explanation:
Using the identity
sin²x + cos²x = 1 ⇒ sin²x = 1 - cos²x
Given
cos²θ - sin²θ = 2 - 5cosθ
cos²θ - (1 - cos²θ) = 2 - 5cosθ
cos²θ - 1 + cos²θ = 2 - 5cosθ
2cos²θ - 1 = 2 - 5cosθ ( subtract 2 - 5cosθ from both sides )
2cos²θ + 5cosθ - 3 = 0 ← in standard form
(cosθ + 3)(2cosθ - 1) = 0 ← in factored form
Equate each factor to zero and solve for θ
cosθ + 3 = 0
cosθ = - 3 ← not possible as - 1 ≤ cosθ ≤ 1
2cosθ - 1 = 0
cosθ =
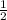 , so
, so
θ =
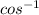 (
(
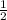 ) =
) =
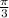 ( or 60° )
( or 60° )