Question

Assume that the Poisson distribution applies and that the mean number of hurricanes in a certain area is 5.1 per year.

a. Find the probability that, in a year, there will be 4 hurricanes.
b. In a 45-year period, how many years are expected to have 4 hurricanes?
c. How does the result from part (b) compare to a recent period of 45 years in which 7 years had 4 hurricanes? Does the Poisson
distribution work well here?
a. The probability is 0.172
(Round to three decimal places as needed.)
b. The expected number of years with 4 hurricanes is 3.62
(Round to one decimal place as needed.)

Answer 1

a) 0.172 probability that, in a year, there will be 4 hurricanes.

b) The expected number of years with 4 hurricanes is 7.7.

c) 7 years is close to the expected value of 7.7, which means that the Poisson distribution works well here.

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

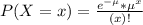
In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given interval.

The mean number of hurricanes in a certain area is 5.1 per year.

This means that
`\mu = 5.1`

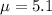
a. Find the probability that, in a year, there will be 4 hurricanes.

This is P(X = 4).

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 4) = (e^(-5.1)*(5.1)^(4))/((4)!) = 0.172`

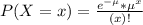
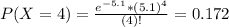
0.172 probability that, in a year, there will be 4 hurricanes.

b. In a 45-year period, how many years are expected to have 4 hurricanes?

Each year, 0.172 probability of 4 hurricanes. So for 45 years, the mean is 45*0.172 = 7.7.

The expected number of years with 4 hurricanes is 7.7.

c. How does the result from part (b) compare to a recent period of 45 years in which 7 years had 4 hurricanes? Does the Poisson distribution work well here?

7 years is close to the expected value of 7.7, which means that the Poisson distribution works well here.