Answer:
D = 54.9 mi, 71.6 South of the East
Step-by-step explanation:
In this exercise it is asked to find the displacement of the body, one of the easiest tasks is to dispose each displacement in a Cartesian coordinate system, let's use trigonometry
* first displacement d₁ = 67.0 mi
the angle is 35 south of east, measured from the axis x θ = -35
cos -35 = x₁ / d₁
sin -35 = y₁ / d₁
x₁ = d₁ cos (-35)
y₁ = d₁ sin (-35)
x₁ = 67 cos 35 = 54.88 mi
y₁ = -67 sin 35 = -38.43 mi
* second displacement d₂ = 40, mi
the angle is 20 to the west of the south, so mean from the axis x is
θ = 180+ 20 = 200º
cos 200 = x₂ / d₂
sin 200 = y₂ / d₂
x₂ = d₂ cos 200
y₂ = d₂ sin 200
x₂ = 40.0 cos 200 = -37.59 mi
y₂ = 40.0 sin 200 = -13.68 mi
now we can find the displacement in each exercise
X_total = x₁ + x₂
X_total = 54.88 -37.59
X_total = 17.29 mi
Y_total = y₁ + y₂
Y_total = -38.43 -13.68
Y_total = - 52.11 mi
Let's use the Pythagorean theorem to find the displacement
D =
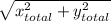
D =
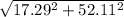
D = 54.9 mi
to find the angle let's use trigonometry
tan θ =
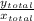
θ = tan⁺¹ \frac{y_{total} }{x_{total} }
θ = tan⁻¹ (-52.11 / 17.29)
θ = -71.6º
the negative sign indicates that it is measured clockwise from the x-axis.
In cardinal coordinates it is 71.6 South of the East