Answer:
The wavelength for the transition from n = 4 to n = 2 is 486nm and the name name given to the spectroscopic series belongs to The Balmer series.
Step-by-step explanation
lets calculate -
Rydberg equation-
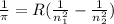
where ,
 is wavelength , R is Rydberg constant (
is wavelength , R is Rydberg constant (
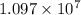 ),
),
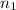 and
and
 are the quantum numbers of the energy levels. (where
are the quantum numbers of the energy levels. (where
 )
)
Now putting the given values in the equation,
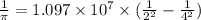

Wavelength
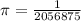
=
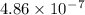 = 486nm
= 486nm
Therefore , the wavelength is 486nm and it belongs to The Balmer series.