Question

A social media website had 350,000 followers in 2010. The number y of followers

increases by 2% each year.
a. Write an exponential growth function that represents the number of followers t
years after 2010
b. How many people will be following the website in 2016? Round your answer to the
nearest thousand.

Answer 1

a)
`y(t) = 350(1.02)^t`

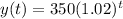
b) 394 thousand = 394,000 people will be following the website in 2016

Explanation:

Exponential equation for an amount:

The exponential equation for an amount after t years has the following format:

`y = y(0)(1+r)^t`

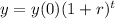
In which y(0) is the initial value and r is the growth rate, as a decimal.

A social media website had 350,000 followers in 2010. The number y of followers increases by 2% each year.

This means that:
`y(0) = 350, r = 0.02`

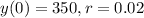
a. Write an exponential growth function that represents the number of followers t years after 2010

In thousands:

`y(t) = 350(1 + 0.02)^t`

`y(t) = 350(1.02)^t`

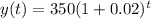
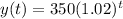
b. How many people will be following the website in 2016?

2016 is 6 years after 2010, so this is y(6).

`y(6) = 350(1.02)^6 = 394.2`

Rounding to the nearest thousand:

394 thousand = 394,000 people will be following the website in 2016