Question

The chance of rain is 20%, the chance of it being sunny is 60%, and the chance of it

being sunny and rainy at the same time is 10%. Calculate, the probability that it is
either sunny or rainy.

Answer 1

0.6 = 60% probability that it is either sunny or rainy.

Explanation:

We solve this question treating these events as Venn probabilities.

I am going to say that:

Event A: Rain

Event B: Sun

The chance of rain is 20%

This means that
`P(A) = 0.2`

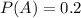
The chance of it being sunny is 60%

This means that
`P(B) = 0.6`

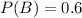
The chance of it being sunny and rainy at the same time is 10%.

This means that
`P(A \cap B) = 0.1`

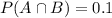
Calculate, the probability that it is either sunny or rainy.

This is:

`P = P(A) + P(B) - 2P(A \cap B) = 0.2 + 0.6 - 0.2 = 0.6`

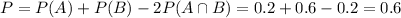
0.6 = 60% probability that it is either sunny or rainy.