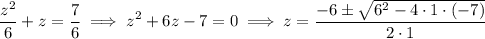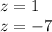Answer:
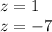
Explanation:
Pretty straightforward question. We have the following definite integral:
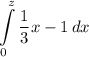
and this integral equals to
 . We want to find the value of
. We want to find the value of

Considering the property that the integral of the sum of functions
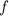 and
and
 equals the integral of
equals the integral of
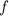 plus the integral of
plus the integral of
 , we have
, we have
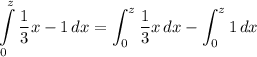
Now we just have to solve each integral.
![$\int _0^z(1)/(3)x \, dx = (1)/(3)\int _0^zx \, dx = \left[(1)/(3)\cdot (x^2)/(2)\right] \Big |_0^z = (x^2)/(6) \Big |_0^z = (z^2)/(6) - (0^2)/(6) =\boxed{ (z^2)/(6)}$](https://img.qammunity.org/2023/formulas/mathematics/high-school/40cnqy8xo3y9wfkm78anxqufzuheqeunfv.png)
Explanation: 1/3 is a constant, that's why we ended up calculating the integral on the given interval for
 . Then, for the integral of
. Then, for the integral of
 I just calculated the antiderivative, given as
I just calculated the antiderivative, given as
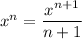 for
for
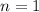 and the Fundamental Theorem of Calculus.
and the Fundamental Theorem of Calculus.
For the other integral, we just have the definite integral of a constant.
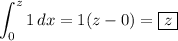
Therefore,
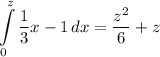
Now we can solve