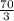Answer:
The Standard form becomes - y =
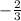 x²
x²
 x +
x +
Explanation:
To find - Write the quadratic function in three forms using the three points it goes through (-1,24),(5,0), and (-4,18)
Proof -
There are there forms of quadratic equation :
1) Standard form: y = ax²+ bx + c
where the a,b, and c are constants
2) Factored form: y = (ax + c)(bx + d)
where a,b,c, and d are constants
3) Vertex form: y = a(x + b)² + c
where a, b, and c are constants
Now,
For Standard form -
Given that the quadratic equation passes through three points
(-1, 24), (5, 0), (-4, 18)
24 = a(-1)²+ b(-1) + c
⇒24 = a - b + c ............(1)
0 = a(5)²+ b(5) + c
⇒0 = 25a + 5b + c ............(2)
18 = a(-4)²+ b(-4) + c
⇒18 = 16a - 4b + c ............(3)
By solving equation (1), (2), (3), we get
a =
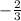 , b =
, b =
 , c =
, c =
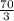
So,
The Standard form becomes - y =
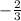 x²
x²
 x +
x +