Question

Need help question #2. Show steps please

Answer 1

C

Explanation:

We want to evaluate the definite integral:

`\displaystyle \int_0^1 (x+2)(3x^2+12x+1)^(1/2)\, dx`

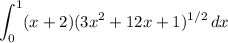
Again, notice that the radicand is quite similar to the outside factor. So, we can use u-substitution again. We will let:

`\displaystyle u=3x^2+12x+1`

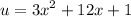
Then:

`\displaystyle (du)/(dx)=6x+12`

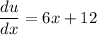
Hence:

`\displaystyle du=6x+12 \, dx`

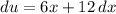
And we can divide both sides by 6:

`\displaystyle (1)/(6)\, du=x+2\, dx`

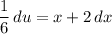
Note that the limits of integration of our original integral (from x = 0 to x = 1) is in the domain of x. Since we changed variables, we should also change the limits of integration to u. So:

`u(0)=3(0)^2+12(0)+1=1`

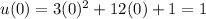
And:

`u(1)=3(1)^2+12(1)+1=16`

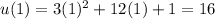
Hence, our new limits of integration is from u = 1 to u = 16.

Perform the substitution:

`\displaystyle =\int_(1)^(16) u^(1/2)\Big((1)/(6)\, du\Big)`

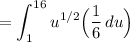
Simplify:

`\displaystyle =(1)/(6)\int_1^(16)u^(1/2)\, du`

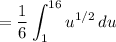
Integrate:

`\displaystyle =(1)/(6)\Big((2)/(3)u^(3/2)\Big)\Big|_(1)^(16)`

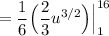
Simplify:

`=\displaystyle (1)/(9)\Big(u^(3/2)\Big|_1^(16)\Big)`

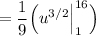
Evaluate:

`\displaystyle =(1)/(9)\Big(16^(3/2)-1^(3/2)\Big)=(1)/(9)(64-1)=7`

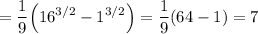
The answer is C.