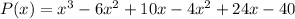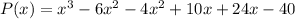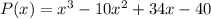Question

Write a polynomial function f of least degree that has rational coefficients, a leading coefficient of 1, and the zeros 4 and 3−i.

Answer 1

`P(x) = x^3 - 10x^2+ 34x-40`

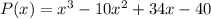
Explanation:

Given

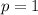`p =1` -- Leading coefficient

`Zeros: 4\ and\ 3 - i`

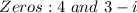
Required

Determine the polynomial

Represent the zeros with a and b

Such that

`a = 4`

`b = 3 - i`

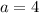
The polynomial is:

`P(x) = p * (x - a) * (x - b)`

`P(x) = 1 * (x - 4) * (x - (3 - i))`

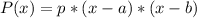
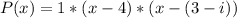
However, to solve further: We need to symmetrise over 3-i and its conjugate

`P(x) = 1 * (x - 4) * (x - (3 - i))* (x - (3 + i))`

`P(x) = (x - 4) * (x - (3 - i))* (x - (3 + i))\\\\`

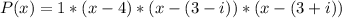
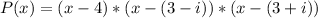
To define a suitable function, the expression becomes

`P(x) = (x - 4) * ((x - 3)^2+1)`

`P(x) = (x - 4) * ((x - 3)(x - 3)+1)`

`P(x) = (x - 4) * (x^2 - 6x + 9+1)`

`P(x) = (x - 4) * (x^2 - 6x +10)`

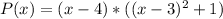
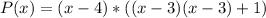
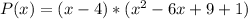
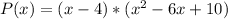
Open bracket

`P(x) = x^3 - 6x^2 +10x - 4x^2 + 24x-40`

`P(x) = x^3 - 6x^2 - 4x^2+10x + 24x-40`

`P(x) = x^3 - 10x^2+ 34x-40`