Question

The ratio R S R T = 1 2 . Point R is at (2, 5) and point T is at (–4, –7). Which could be the coordinates of S? A. (–1, –1)

Answer 1

The coordinates of the point S could be;

A. (-1, -1)

Explanation:

The given parameters are;

The ratio of the length of the line RS to the length of the line RT = 1:2

The coordinates of point R = (2. 5)

The coordinates point T = (-4, -7)

Therefore, we have;

`(The \ length \ of \, RS)/(The \ length \ of \, RT) = (1)/(2)`

`\therefore {The \ length \ of \, RS} = (1)/(2) * The \ length \ of \, RT`

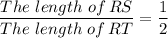
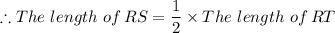
The length of the line RT = √(((2 - (-4))² + (5 - (-7))²) = 6·√5

Therefore, we have;

`{The \ length \ of \, RS} = (1)/(2) * 6\cdot √(5) = 3 \cdot √(5)`

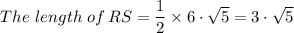
When the coordinates of the point S = (-1, -1), we have;

The length of the line RS = √(((2 - (-1))² + (5 - (-1))²) = √45 = 3·√5

Therefore, the coordinates of the point S could be (-1, -1)