Answer:
Work = 165670.4 J = 165.67 KJ
Step-by-step explanation:
First, we will find the deceleration of the car, using the 3rd equation of motion:
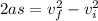
where,
a = deceleration = ?
s = skid distance = 40 m
vf = final speed = 0 m/s
vi = initial speed = 17.2 m/s
Therefore,
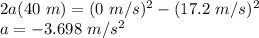
the negative sign indicates deceleration here.
Now, we will calculate the braking force applied by the brakes on the car:
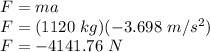
the negative sign indicates braking force.
Now, we will calculate the work done using the magnitude of this force:
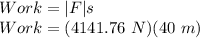
Work = 165670.4 J = 165.67 KJ