Answer:
#1: The measure of m<B is 125°.
#2: M<Y is equal a 27°.
#3: So the length of DF is 5.99 km.
#4: the side length AC is 13.1 feet.
Step-by-step explanation:
# 1: The following given,
c = AB = 17 cm
a = BC = unknown
b = CA = 44 cm
Ø = 125
M<B means it is the angle at vertex B of the triangle, it is also the only angle given in thbe figure.
Therefore, The measure of m<B is 125°.
#2: We can calculate the value of the angles by means of the law of sine which is the following:
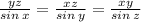
We need you know the Y value, therefore we replace and solve for Y
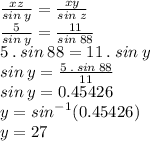
#3: In order to find the length of Df, we can use the law of sines in this triangle:
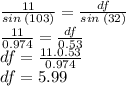
So the length of DF is 5.99 km.
#4: We are given two two angles and one side length.
<A = 37°
<B = 65°
AB = 13 ft
We are asked to find side length AC
We can use the "law of sines" to find the side length AC
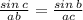
Let us first find the angle <C
Recall that the sum of all three interior angles of a triangle must be equal to 180°
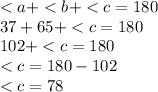
So, the angle <C is 78°
Now let us substitute all the known values into the law of sines formula and solve for AC

Therefore, the side length AC is 13.1 feet.