Answer:
9 mph
Explanation:
Speed of current = 6 mph
Distance to travel one way = 22.5 miles
Let speed of the ferry be
 mph
mph
Total time taken for round trip is 9 hours
One way the ferry will be going with the current and in the other way the ferry will be going against the current so
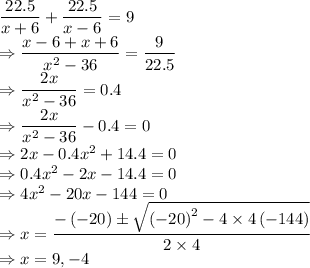
So, the speed of the boat in still water needs to be 9 mph both ways.