Final answer:
To calculate the monthly withdrawal, we first find the future values of monthly investments in both stock and bond accounts over a 35-year period and then combine these amounts. We use these combined funds to calculate the monthly withdrawal using the annuity formula based on the 6.1% annual return expected during the 30-year retirement period.
Step-by-step explanation:
To determine how much can be withdrawn each month from the retirement account during the 30-year withdrawal period, we need to first calculate the future value of the monthly investments in the stock and bond accounts over the 35-year accumulation period. We will then combine these values and use the annuity formula to calculate the monthly withdrawal amount.
Stock Account Accumulation
The future value of the stock account is calculated using the formula for the future value of an annuity due to regular monthly investments:
FV = P × × (
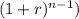 / r)
/ r)
Where:
- P = monthly investment
- r = monthly interest rate
- n = total number of payments
For the stock account:
- P = $710
- r = 9.1% annual interest rate, so the monthly rate is 0.091 / 12
- n = 35 years × 12 months/year
Bond Account Accumulation
Similarly, for the bond account:
- P = $310
- r = 5.1% annual interest rate, so the monthly rate is 0.051 / 12
- n = 35 years × 12 months/year
After calculating the future values for both accounts, you'll sum them up and then use the annuity formula to determine the monthly withdrawal:
Withdrawal = Total Accumulated Value × (r ×
 ) / (
) / (
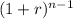 )
)
Where r is the monthly retirement account interest rate (6.1% annual rate => 0.061 / 12 per month) and n is the total number of withdrawals (30 years × 12 months/year).
Note that you would first calculate the future value of both the stock and bond accounts separately, combine them, and then use that combined value to calculate the monthly withdrawal using the specified retirement account return rate and the 30-year period.