Answer:
-3 and 10
Explanation:
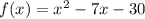
1) Factor the equation
First, find two factors of -30 which has a sum of -7.
⇒ These two factors are 3 and -10.
Then, write the equation as a product of two binomials.
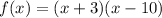
2) Find the zeros
The zero product property states that any value, when multiplied by 0 will equal 0. Therefore, in this equation, either x+3 or x-10 must equal 0 for the function to equal 0:
x+3=0
x=-3
or
x-10=0
x=10
Therefore, the zeros of the function are -3 and 10.
I hope this helps!