Question

A swimming pool is treated periodically to control harmful bacteria growth.

The concentration of bacterial per cm³ after t days is given by
C(t)

`= 30t^2 -240t + 500`
in how many days after a treatment will be concentration be minimal ?
​

Answer 1

The answer is 4

Explanation:

`c \: (t) = {30ft}^(2) = - 240t + 500`

For a quadratic function as given to find the minimum you need to write it in vertex or find the vertex (the vertex in a quadratic function is thr maximum or minimum).

Use the next formula to find the t coordinate of the vertex (the time in the minimum concentration of bateria):

`c \: (t) = {at}^(2) + bt + c \\ \\ tm = - (b)/(2a)`

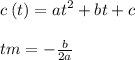
For the given function:

`tm = - ( - 240)/((2)30) = (240)/(60) = 4`

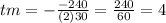
The minimum concentration of bacteria will be after 4 days.