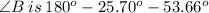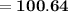Answer:
See below
Explanation:
to understand this
you need to know about:
- law of sine
- law of cosine
- PEMDAS
let's solve:
there are 3 ways to solve SAS triangle
- use The Law of Cosines to calculate the unknown side,
- then use The Law of Sines to find the smaller of the other two angles
- and then use the three angles add to 180° to find the last angle.
first figure out
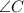
to do so we will use the formula of law of cosine of C angle
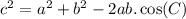
substitute the given values of a,b and
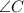
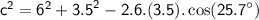
simplify squares:
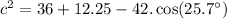
simplify addition:
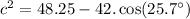
square root both sides
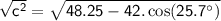
simplify:
therefore
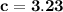
use law of sine to figure out angle A
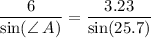
therefore
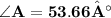 (use calculater to simplify it)
(use calculater to simplify it)
therefore