The scale factor from
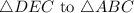 is 8:25, and the value of x is 4.
is 8:25, and the value of x is 4.
To find the value of x and the scale factor from
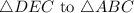 , we can use the fact that corresponding sides of congruent triangles are in proportion.
, we can use the fact that corresponding sides of congruent triangles are in proportion.
Let AB = 3x - 2 and DE = 2x.
According to the proportionality of corresponding sides:
![\[(AB)/(DE) = (AC)/(CD)\]](https://img.qammunity.org/2022/formulas/mathematics/high-school/p8sh1z2pb4396sl2wtl2jgxfl0mpttdf8s.png)
Substitute the given values:
![\[(3x - 2)/(2x) = (25)/(20)\]](https://img.qammunity.org/2022/formulas/mathematics/high-school/pabtfay9vxtfijpvpi4faydr6p0c59soci.png)
Now, solve for x:
![\[20(3x - 2) = 25(2x)\]](https://img.qammunity.org/2022/formulas/mathematics/high-school/3cw4qkxmuf83gnh1acur71if5rgrewk5mo.png)
Distribute and simplify:
![\[60x - 40 = 50x\]](https://img.qammunity.org/2022/formulas/mathematics/high-school/qz29qgoftoa0hr30vzb1n39ja4w645yeus.png)
Subtract 50x from both sides:
![\[10x - 40 = 0\]](https://img.qammunity.org/2022/formulas/mathematics/high-school/nn86y5jtbl444tckm3wgk3mj52jpwmp6ui.png)
Add 40 to both sides:
![\[10x = 40\]](https://img.qammunity.org/2022/formulas/mathematics/high-school/j5k6obldkip6pe0pv3dskxvu96uzaobo0f.png)
Divide by 10:
![\[x = 4\]](https://img.qammunity.org/2022/formulas/mathematics/high-school/k8le6zynyv49zrh1279fumeyzmas8e9p93.png)
So, x = 4.
Now, to find the scale factor, substitute x back into the expression for DE:
![\[DE = 2x = 2 * 4 = 8\]](https://img.qammunity.org/2022/formulas/mathematics/high-school/qpwn5al56qwa118pwks85o79ut75nb1eo9.png)
The scale factor from
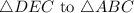 is 8:25, and the value of x is 4.
is 8:25, and the value of x is 4.