Question

Given that P = (2, 9) and Q = (4, 14), find the component form and magnitude of vector PQ . (1 point) <2, 5>, square root of twenty nine <-2, -5>, 29 <2, 5>, 29 <-2, -5>, square root of twenty nine

Answer 1

Given:

The two endpoints of a vector are P = (2, 9) and Q = (4, 14).

To find:

The component form and magnitude of vector PQ .

Solution:

A vector is defined as

`v=\left<x_2-x_1,y_2-y_1\right>`

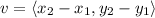
Where,
`(x_1,y_1)` is the initial point and
`(x_2,y_2)` is the terminal point.

Two endpoints of a vector are P = (2, 9) and Q = (4, 14). So, the vector PQ is

`\overrightarrow{PQ}=\left<4-2,14-9\right>`

`\overrightarrow{PQ}=\left<2,5\right>`

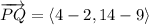
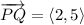
Component form of vector PQ is
`\left<2,5\right>`.

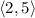The magnitude of a vector
`v=\left<a,b\right>` is

`|\vec{v}|=√(a^2+b^2)`

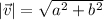
The magnitude of vector PQ is:

`|\overrightarrow{PQ}|=√(2^2+5^2)`

`|\overrightarrow{PQ}|=√(4+25)`

`|\overrightarrow{PQ}|=√(29)`

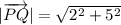
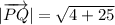
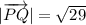
Therefore, the correct option is A.