Question

B) The cost (x) for hiring and artist for a stage show for (y) hours is represente

as 2y + x = 20.
Draw the graph 2y + x = 20 on the grid below.
[4]​

Answer 1

The easiest way is to transform this equation to intercept form of straight line.

`\\`

Intercept form of straight line:

• 
  `(x)/(a)+(y)/(b)=1`

where
`a` is the x intercept - where the graph intersects the x axis, and
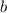`b` is the y intercept - where the graph intersects the y axis.

`\\`

Given that,

`2y + x = 20`

`\longrightarrow \: (2)/(20)y + (x)/(20) = 1`

`\longrightarrow \: (x)/(20) + (y)/(10) = 1`

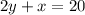
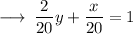
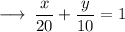
On comparing with
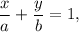`(x)/(a)+(y)/(b)=1,` we get,

• 
  `a=20`
• 
  `b=10`

Hence, the graph shall cut the x axis and y axis at 20 and 10 respectively. This information is enough to plot the graph.

`\\`

Graph: Refer to the attachment.