Question

ABC is a triangle.

A
B.
Diagram NOT
accurately drawn
6 cm
7 cm
60°
C С
Work out the length of the side AB.
Give your answer correct to 3 significant figures.
(3 marks)
O AB=
cm
i okk

Answer 1

A graph has quantity on the x-axis and price on the y-axis. A supply line goes through (10, 25), (20, 30), (30, 35), (40, 40).A graph has quantity on the x-axis and price on the y-axis. A demand line goes through (10, 40), (20, 30), (30, 20), (40, 10). Based on the supply graph and the demand graph shown above, what is the price at the point of equilibrium? a. 20 b. 30 c. 40 d. There is not enough information given to determine the point of equilibrium. Please select the best answer from the choices provided A B C D

Answer 2

The length of side AB is approximately 6.56 cm.

To find the length of side AB in triangle ABC, you can use the Law of Cosines. The Law of Cosines is given by:

`\[ c^2 = a^2 + b^2 - 2ab \cos(C) \]`

Where:

- c is the length of the side opposite angle C (side BC),

- a and b are the lengths of the other two sides (sides AB and AC),

- c is the measure of angle C.

In this case, you want to find the length of side AB, so a is the side opposite angle A, b is the side opposite angle B, and c is the side opposite angle C.

Given:

- AB = a = 6 cm

- BC = c = 7 cm

- angle C =
`60^\circ \)`

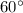
Substitute these values into the Law of Cosines:

`AB^2 = AC^2 + BC^2 - 2 \cdot AC \cdot BC \cdot \cos(C) \]\\AB^2 = 6^2 + 7^2 - 2 \cdot 6 \cdot 7 \cdot \cos(60^\circ) \]\\AB^2 = 36 + 49 - 2 \cdot 6 \cdot 7 \cdot (1)/(2) \]\\AB^2 = 85 - 42 \]\\AB^2 = 43 \]`

Now, take the square root of both sides to solve for AB:

`\[ AB = √(43) \]`

Using a calculator, you get:

`\[ AB \approx 6.557 \]`

Rounded to three significant figures, the length of side AB is approximately 6.56 cm.