Given:
A train is traveling at a constant speed in miles per hour.
The table of value is:
Hours (x) Miles (y)
1 20
2 100
3 180
4 260
5 340
To find:
The equation for the given data table.
Solution:
It is given that the train is traveling at a constant speed in miles per hour. So, it is a linear relationship.
Choose any two point from the given table of value. Let the two points are (1,20) and (2,100). So, the equation of the line is:
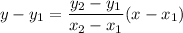
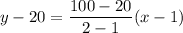
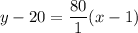
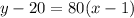
Add 20 on both sides.
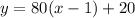
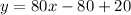
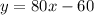
Therefore, the correct option is D.