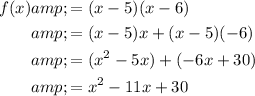Question

Write the equation, in standard form of the quadratic relation

Zeros of 5 and 6 and a y-intercept of 30

Answer 1

`f(x)=x^2-11x+30`

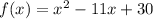
Explanation:

The factored form of a quadratic is given by:

`f(x)=a(x-p)(x-q)`

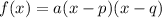
Where p and q are the zeros, and a is the leading coefficient.

The quadratic relation has zeros of 5 and 6, and it has a y-intercept of 30.

Since the zeros are 5 and 6, p and q are 5 and 6. Thus:

`f(x)=a(x-5)(x-6)`

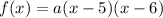
The y-intercept is 30. In other words, when x = 0, f(x) = 30:

`30=a(0-5)(0-6)`

Solve for a:

`30=a(-5)(-6)\Rightarrow 30=30a\Rightarrow a=1`

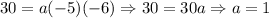
Therefore, our quadratic in factored form is:

`f(x)=(x-5)(x-6)`

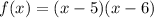
To find the standard form, expand:

`\begin{aligned} f(x)&=(x-5)(x-6)\\&= (x-5)x+(x-5)(-6)\\&=(x^2-5x)+(-6x+30)\\&=x^2-11x+30\end{aligned}`