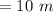Answer:
The correct solution is option A "10 meters".
Step-by-step explanation:
The given values are:
Wave X,
Frequency,
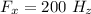
Wavelength
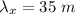
Wave Y,
Frequency,
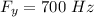
Let its wavelength =
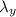
As we know,
⇒
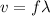
For both waves, medium is same then
⇒
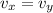
⇒
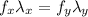
then,
⇒
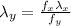
On substituting the estimated values in the above equation, we get
⇒
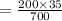
⇒
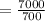
⇒