Question

1 4 (12푥푥 + 24) − 9푥푥 and −6(푥푥 + 1) are equivalent. Is she correct?

Answer 1

No, Gloria is not correct. The solution for the first expression "-6x + 6", is not equivalent to the second expression's solution "-6x - 6".

Explanation:

`( 1 )/( 4 ) \left( 12x+24 \right)-9x`

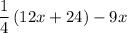
Use the distributive property to multiply
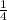`(1)/(4)` by 12x + 24

`( 1 )/( 4 ) * 12x+ ( 1 )/( 4 ) * 24-9x`

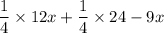
Multiply
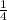`(1)/(4)` and 12 to get
`(12)/(4)`

`( 12 )/( 4 ) x+ ( 1 )/( 4 ) * 24-9x`

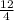
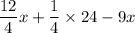
Divide 12 by 4 to get 3

`3x+ ( 1 )/( 4 ) * 24-9x`

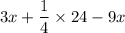
Multiply
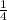`(1)/(4)` and 24 to get
`(24)/(4)`

`3x+ ( 24 )/( 4 ) -9x`

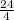
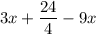
Divide 24 by 4 to get 6

`3x + 6-9x`

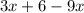
Combine 3x and -9x to get -6x

-6x + 6

So the answer for the first expression is -6x + 6

Now lets solve the second expression

-6 ( x + 1)

Use the distributive property to multiply −6 by x + 1

-6x - 6

So the answer for the second expression is -6x - 6

So we can conclude that the two expressions are not equivalent