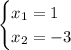Question

Axis of sym: x =

Vertex: (
,
)

Do not do the domain

Range: Pick one: A. y≥4 B. y<4 C. y≤4 D. y≤−2 E. y<−2

The Range is

Zeros:
and


Equation:

Answer 1

SEE BELOW

Explanation:

to understand this

you need to know about:

• quadratic function
• PEMDAS

let's solve:

vertex:(h,k)

therefore

vertex:(-1,4)

axis of symmetry:x=h

therefore

axis of symmetry:x=-1

• to find the quadratic equation we need to figure out the vertex form of quadratic equation and then simply it to standard form i.e ax²+bx+c=0

vertex form of quadratic equation:

• y=a(x-h)²+k

therefore

• y=a(x-(-1))²+4
• y=a(x+1)²+4

it's to notice that we don't know what a is

therefore we have to figure it out

the graph crosses y-asix at (0,3) coordinates

so,

3=a(0+1)²+4

simplify parentheses:

`3 = a(1 {)}^(2) + 4`

simplify exponent:

`3 = a + 4`

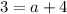
therefore

`a = - 1`

our vertex form of quadratic equation is

• y=-(x+1)²+4

let's simplify it to standard form

simplify square:

`y = - ( {x}^(2) + 2x + 1) + 4`

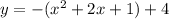
simplify parentheses:

`y = - {x}^(2) - 2x - 1 + 4`

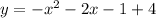
simplify addition:

`y = - {x}^(2) - 2x + 3`

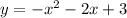
therefore our answer is D)y=-x²-2x+3

the domain of the function

`x\in \mathbb{R}`

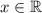
and the range of the function is

`y\leqslant 4`

zeroes of the function:

`- {x}^(2) - 2x + 3 = 0`

`\sf divide \: both \: sides \: by \: - 1`

`{x}^(2) + 2x - 3 = 0`

`\implies \: {x}^(2) + 3x - x + 3 = 0`

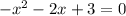
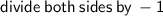
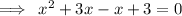
factor out x and -1 respectively:

`\sf \implies \: x(x + 3) - 1(x + 3 )= 0`

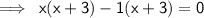
group:

`\implies \: (x - 1)(x + 3) = 0`

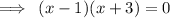
therefore

`\begin{cases} x_(1) = 1 \\ x_(2) = - 3\end{cases}`