Question

F(x)=4^x and g(x)=4^x+2

State the type of transformation from f(x) to g(x) in the problem above and including its distance moved.

Answer 1

Given:

The two functions are:

`f(x)=4^x`

`g(x)=4^x+2`

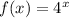
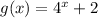
To find:

The type of transformation from f(x) to g(x) in the problem above and including its distance moved.

Solution:

The transformation is defined as

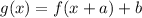`g(x)=f(x+a)+b` .... (i)

Where, a is horizontal shift and b is vertical shift.

• If a>0, then the graph shifts a units left.
• If a<0, then the graph shifts a units right.
• If b>0, then the graph shifts b units up.
• If b<0, then the graph shifts b units down.

We have,

`f(x)=4^x`

`g(x)=4^x+2`

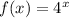
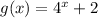
The function g(x) can be written as

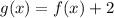`g(x)=f(x)+2` ...(ii)

On comparing (i) and (ii), we get

`a=0,b=2`

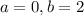
Therefore, the type of transformation is translation and the graph of f(x) shifts 2 units up to get the graph of g(x).