Answer:
a)
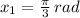 ,
,
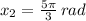 , b)
, b)
 ,
,
 ,
,
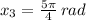 ,
,

Explanation:
a) We proceed to solve the expression by algebraic and trigonometrical means:
1)
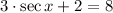
2)

3)
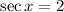
4)
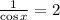
5)
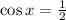
6)
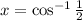
Cosine has positive values in first and fourth quadrants. Then, we have the following two solutions:
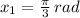 ,
,
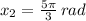
b) We proceed to solve the expression by algebraic and trigonometrical means:
1)
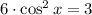
2)
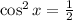
3)
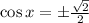
4)
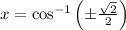
There is one solution for each quadrant. That is to say:
 ,
,
 ,
,
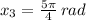 ,
,
