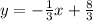Answer:
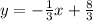
Explanation:
Given
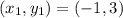
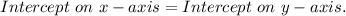
Required
Determine the equation
First, we calculate the intercepts using:
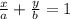
Where
b = Intercept on y axis.
a = Intercept on x axis.
From the question:
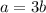
The equation becomes:
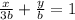
Multiply through by 3b
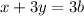
We have:
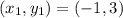
So:


Make b the subject
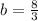
Substitute
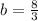 in
in
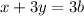 to get the equation
to get the equation
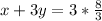
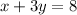
Make 3y the subject
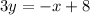
Make y the subject