Answer:
The deceleration is -7.85x10³ rad/s².
Step-by-step explanation:
The angular speed (ω) is related to frequency (f) as follows:
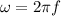
When the frequency is 30 Hz the angular speed is:
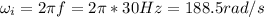
Now, when the frequency is 20 Hz the angular speed is:
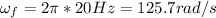
Finally, the angular acceleration (α) can be found using the following equation:
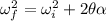
Where:
θ: is the angular displacement = 72°
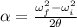
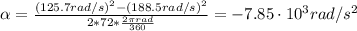
Therefore, the deceleration is -7.85x10³ rad/s².
I hope it helps you!