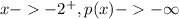Question

Describe the behavior of the function ppp around its vertical asymptote at x=-2x=−2x, equals, minus, 2. ​

Answer 1

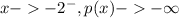`x->-2^(-), p(x)->-\infty` and as
`x->-2^(+), p(x)->-\infty`

Explanation:

Given

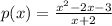`p(x) = (x^2-2x-3)/(x+2)` -- Missing from the question

Required

The behavior of the function around its vertical asymptote at
`x = -2`

`p(x) = (x^2-2x-3)/(x+2)`

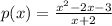
Expand the numerator

`p(x) = (x^2 + x -3x - 3)/(x+2)`

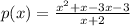
Factorize

`p(x) = (x(x + 1) -3(x + 1))/(x+2)`

Factor out x + 1

`p(x) = ((x -3)(x + 1))/(x+2)`

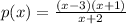
We test the function using values close to -2 (one value will be less than -2 while the other will be greater than -2)

We are only interested in the sign of the result

----------------------------------------------------------------------------------------------------------

As x approaches -2 implies that:

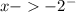`x -> -2^(-)` Say x = -3

`p(x) = ((x -3)(x + 1))/(x+2)`

`p(-3) = ((-3-3)(-3+1))/(-3+2) = (-6 * -2)/(-1) = (+12)/(-1) = -12`

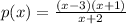
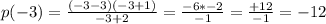
We have a negative value (-12); This will be called negative infinity

This implies that as x approaches -2, p(x) approaches negative infinity

`x->-2^(-), p(x)->-\infty`

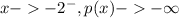
Take note of the superscript of 2 (this implies that, we approach 2 from a value less than 2)

As x leaves -2 implies that:
`x>-2`

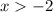
Say x = -2.1

`p(-2.1) = ((-2.1-3)(-2.1+1))/(-2.1+2) = (-5.1 * -1.1)/(-0.1) = (+5.61)/(-0.1) = -56.1`

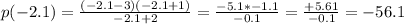
We have a negative value (-56.1); This will be called negative infinity

This implies that as x leaves -2, p(x) approaches negative infinity

`x->-2^(+), p(x)->-\infty`

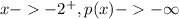
So, the behavior is:

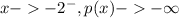`x->-2^(-), p(x)->-\infty` and as
`x->-2^(+), p(x)->-\infty`